Nernst Equation
Introduction
Electrochemistry is the study of both the potential of individual cells and the energy released by chemical processes. The movement of charges is caused by the energy that is present in a chemical system, and the force that causes the charges to move is what gives birth to the cell potential in a system that is known as a galvanic cell. The issue of energy is also connected to the chemical equilibrium in some way. The idea of the Nernst equation is what binds all of these connections together into one cohesive whole.

In appreciation of his contributions to the field of thermochemistry, Walther H. Nernst (1864-1941) was awarded the Nobel Prize in Chemistry in 1920. Because of his contribution to chemical thermodynamics, a well-known equation was developed that establishes a correlation between the amount of chemical energy and the electric potential of a galvanic cell or battery.
All transformations, including chemical processes, are driven by energy. A potential difference is created whenever there is a redox reaction because the movement of charged particles results in the release of energy during the reaction. The electromotive force, also known as E, is the greatest potential difference, and the maximum electric work, W, is equal to the product of the charge, measured in Coulombs (C), and the potential, measured in volts (= joules per coulomb), also known as EMF.
WJ=qDECJ/C(units)
Take note that the EMF DE is not decided by the size of the cell or the quantity of material that are contained inside it; rather, it is defined by the type of the reactants and electrolytes. The charge on the galvanic cell and the quantity of energy it has available are both proportional to the number of reactants that are used.
The Gibb’s free energy DG is the negative value of maximum electric work,
ΔG=−W=−qΔE
A redox reaction equation represents definite amounts of reactants in the formation of also definite amounts of products. The number (n) of electrons in such a reaction equation is related to the amount of charge transferred when the reaction is completed. Since each mole of electron has a charge of 96485 C (known as the Faraday’s constant, F),
q=nF
ΔG=−nFΔE
ΔG∘=−nFΔE∘ (at standard conditions)
The general Nernst equation correlates the Gibb’s Free Energy DG and the EMF of a chemical system known as the galvanic cell. For the reaction
The General Nernst Equation
The general Nernst equation correlates the Gibb’s Free Energy DG and the EMF of a chemical system known as the galvanic cell. For the reaction
aA+bB⇌cC+dD
ΔG = ΔGo + RT ln Q
ΔG = -nFΔE
-nFΔE=-nFΔEo + RT lnQ
Where R, T, Q and F are the gas constant (8.314J mol-1 K-1), temperature (K), reaction quotient and Faraday Constant (96485 C) respectively. Accordingly, we have
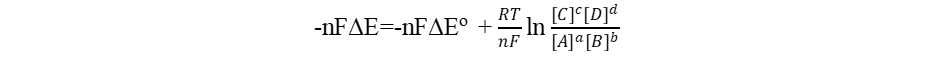
This is known as the Nernst equation. The equation allows us to calculate the cell potential of any galvanic cell for any concentrations. Some examples are given in the next section to illustrate its application.
It is interesting to note the relationship between equilibrium and the Gibb’s free energy at this point. When a system is at equilibrium, ΔEo = 0, and Qeq = K. Therefore, we have,
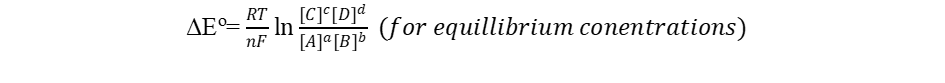
Thus, the equilibrium constant and ΔEo are related.
The Nernst Equation at 298 K
The Nernst equation derived above can be reduced to a simple form at any specific temperature. For example, at the standard condition of 298 K (25°), the Nernst equation becomes
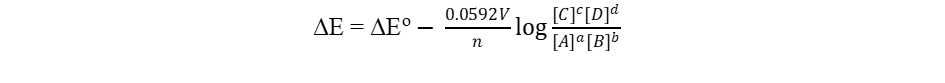
Please note that log is the logarithm function based 10, and ln, the natural logarithm function.
For the cell
Zn\Zn2+ \\ H+\H2\Pt
The overall chemical reaction is
Zn(s) + 2H+ Zn2+ + H2 (g)
The standard cell potential ΔEo = 0.763
Suppose, the concentration of the ions are no 1.0M, and the H2 pressure is not 1.0 atm, then the cell potential ΔE may be calculated using the Nernst equation:
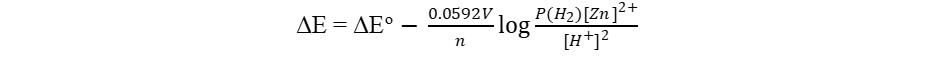
with n equal to 2 since the process includes two electrons. The value is 0.0592 only when T = 298 degrees Kelvin. This constant varies with temperature. Note that the reactivity of solid Zn is considered to be 1. If the pressure of H2 equals 1 atmosphere, the phrase P(H2) may likewise be deleted. The argument expression for the log function follows the same principles as expressions for equilibrium constants and reaction quotients.
In fact, the argument for the log function is the equilibrium constant K or reaction quotient Q expression.
When a cell is in equilibrium, ΔE = 0.00 and the expression becomes a constant of equilibrium, K, whose connection is as follows:
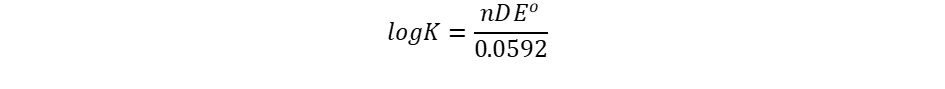
where ΔEo is the difference between the standard potentials of the concerned half cells. Any voltage-containing battery is not in balance.
The Nernst equation also suggests that a battery may be constructed by using the same material for both cells but at different concentrations. These cells are known as concentration cells.
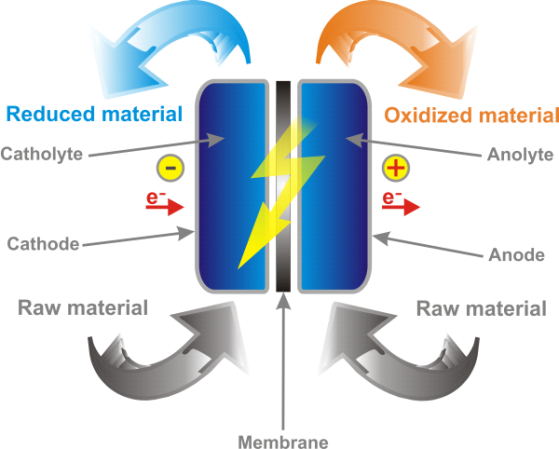
Common misconceptions in electrochemistry: Galvanic, electrolytic, and concentration cells
Here are some common student misconceptions in electrochemistry:
- Confusing Galvanic and Electrolytic cells: One of the most common misconceptions is that Galvanic cells and Electrolytic cells are the same thing. Galvanic cells produce electricity from spontaneous redox reactions, whereas Electrolytic cells use electrical energy to drive non-spontaneous redox reactions. It is important to understand the key differences between these two types of cells.
- Misunderstanding the direction of electron flow: Another common misconception is the direction of electron flow in a cell. Electrons always flow from the anode (where oxidation occurs) to the cathode (where reduction occurs). However, students often think that electrons flow from the cathode to the anode.
- Misunderstanding the role of salt bridges: Salt bridges are used in cells to maintain charge neutrality by allowing the flow of ions between the two compartments of the cell. However, students often think that the salt bridge is used to complete the circuit, which is not true. The salt bridge does not conduct electricity; it only allows the flow of ions.
- Confusing the sign of the cell potential: The sign of the cell potential indicates the direction of electron flow and the spontaneity of the redox reaction. However, students often confuse the sign of the cell potential and mistakenly think that a positive cell potential always means the reaction is exothermic or that a negative cell potential always means the reaction is endothermic.
- Misunderstanding concentration cells: A concentration cell is a type of Galvanic cell where the same metal is used as both the anode and cathode, but the concentrations of the metal ions in each half-cell are different. Students often think that concentration cells produce electrical energy from a spontaneous redox reaction, but this is not the case. In a concentration cell, electrical energy is used to move ions from one half-cell to the other until the concentrations of the metal ions are equal, and the cell reaches equilibrium.
Nernst Equation in electrochemical applications
The Nernst equation is a fundamental tool used in electrochemistry to describe the relationship between the concentration of an electroactive species and the potential of an electrochemical cell. It is named after Walther Nernst, a German physical chemist who developed the equation in 1889. In simple terms, the Nernst equation provides a way to calculate the potential of an electrochemical cell at non-standard conditions.
The Nernst equation is based on the principle of the equilibrium of the electrochemical reaction taking place in the cell. It states that the potential of an electrochemical cell, E, is related to the concentrations of the reactants and products involved in the cell reaction, as well as their standard electrode potentials. Mathematically, the Nernst equation can be expressed as:
E = E° – (RT/nF) ln(Q)
where E is the cell potential at non-standard conditions, E° is the standard electrode potential, R is the gas constant, T is the absolute temperature, n is the number of electrons transferred in the reaction, F is the Faraday constant, and Q is the reaction quotient.
The Nernst equation has numerous applications in electrochemistry, ranging from analytical chemistry to industrial processes. Here are some examples:
- pH measurements: The Nernst equation is used to calculate the potential of a pH electrode, which is a type of electrochemical cell used to measure the pH of a solution. The pH electrode contains a thin glass membrane that separates an acidic or basic solution from a reference solution. The potential difference between the two solutions is proportional to the pH of the sample solution.
- Batteries: The Nernst equation is used to calculate the cell potential of a battery at non-standard conditions. For example, if the concentration of reactants or products changes due to discharge or charging, the Nernst equation can be used to predict the resulting cell potential.
- Corrosion: The Nernst equation is used to calculate the corrosion potential of a metal in a corrosive environment. The corrosion potential is the potential at which the metal corrodes at a specific rate. By measuring the potential of a metal electrode in a corrosive environment, it is possible to predict the rate of corrosion and develop strategies to prevent it.
- Bioelectrochemistry: The Nernst equation is used to study the electrochemical reactions that take place in living organisms. For example, the Nernst equation can be used to calculate the potential difference across the cell membrane of a neuron, which is essential for the transmission of electrical signals.
- Electroplating: The Nernst equation is used to calculate the potential of an electroplating cell, which is a type of electrochemical cell used to deposit a metal coating on a substrate. The potential difference between the anode and cathode electrodes determines the rate of deposition and the quality of the coating.
In conclusion, the Nernst equation is a versatile tool that has a wide range of applications in electrochemistry. It allows scientists and engineers to predict the behavior of electrochemical systems at non-standard conditions and to design and optimize electrochemical processes for a variety of applications.